FormalGeo: Formal representation and solving for Euclidean plane geometry problems

FormalGeo is a framework for formal representation and solving of plane geometry, encompassing the entire workflow including theory, formal systems, reasoning-computation engines, datasets, evaluation metrics, and neural-symbolic solvers. FormalGeo is currently maintained by the FormalGeo Development Team, an open-source research organization dedicated to advancing the frontiers of artificial intelligence through formal mathematical reasoning. We primarily focus on automatically Geometry Problem-Solving at or beyond the difficulty of the International Mathematical Olympiad (IMO) to explore the boundaries of machine abstraction and reasoning.

Plane geometry, characterized by its multimodal knowledge representation, rigorous axiomatic structure, and reliance on spatial intuition, serves as a natural benchmark for evaluating an AI system’s capabilities in perception, comprehension, and logical deduction. We aim to empower machines with mathematical reasoning abilities that match or surpass those of humans, thereby establishing a new paradigm for General Artificial Intelligence that integrates Symbolism, Connectionism, and Behaviorism. Our goal is to construct a verifiable, interpretable, and scalable system for automated Geometric Knowledge Discovery (GKD) and Geometric Problem-Solving (GPS), laying the foundation for AI-driven mathematical discovery, formal verification, and intelligent education.

FormalGeo, established in 2022, has developed into a comprehensive and closed-loop research framework for formal plane geometry. In April 2026, we released FormalGeo-beta, a new solver version that unifies geometric configuration construction, problem-solving, and solution generation. By integrating modern neuro-symbolic architectures, the vision of building a geometric problem-solving system that surpasses human performance is becoming a reality.

FormalGeo is currently maintained by the FormalGeo Development Team. We are committed to open-source and welcome contributions from the community. We look forward to having more people become part of this incredible journey.

News

[Apr 06, 2026] 💥FormalGeo-beta has been released, supporting auxiliary construction and bidirectional solving (fact derivation and goal decomposition). For details, please check the FormalGeo GitHub Project.
[Mar 30, 2026] 💥Paper "A Hybrid Framework for Automated Geometric Problem-Solving by Integrating Formal Symbolic Systems and Deep Learning" is accepted by Symmetry 2026.
[Jun 07, 2025] Paper "FGeo-Eval: Evaluation System for Plane Geometry Problem Solving" is accepted by Symmetry 2025.
[Jun 05, 2025] We have been invited by Professor Hanchuan Peng to give an academic presentation at Fudan University.
[Apr 29, 2025] Paper "FGeo-HyperGNet: Geometric Problem Solving Integrating FormalGeo Symbolic System and Hypergraph Neural Network" is accepted by IJCAI 2025.
[Dec 22, 2024] Paper "Diagram Formalization Enhanced Multi-Modal Geometry Problem Solver" is accepted by ICASSP 2025.
[Dec 19, 2024] Paper "FGeo-Parser: Autoformalization and Solution of Plane Geometric Problems" is accepted by Symmetry 2025.
[Nov 02, 2024] We have been invited to give an academic presentation at The Chinese Mathematical Society 2024 Annual Academic Conference.
[Oct 12, 2024] We have been invited to give an academic presentation at ForICM 2024.
[Oct 10, 2024] Paper "Formal Representation and Solution of Plane Geometric Problems" is accepted by NeurIPS 2024 Workshop on MATH-AI.
[May 24, 2024] We have been invited to give an academic presentation at Shanghai Center for Mathematical Sciences.
[May 15, 2024] We have been invited by Professor Bican Xia to give an academic presentation at Peking University.
[Apr 05, 2024] Paper "FGeo-DRL: Deductive Reasoning for Geometric Problems through Deep Reinforcement Learning" is accepted by Symmetry 2024.
[Apr 03, 2024] Paper "FGeo-TP: A Language Model-Enhanced Solver for Geometry Problems" is accepted by Symmetry 2024.
[Mar 30, 2024] Paper "FGeo-SSS: A Search-Based Symbolic Solver for Human-Like Automated Geometric Reasoning" is accepted by Symmetry 2024.
[Feb 20, 2024] Paper "FGeo-HyperGNet: Geometry Problem Solving Integrating Formal Symbolic System and Hypergraph Neural Network" is available at Preprint.
[Feb 15, 2024] Paper "FGeo-DRL:Deductive Reasoning for Geometric Problems through Deep Reinforcement Learning" is available at Preprint.
[Feb 15, 2024] Paper "FGeo-TP: A Language Model-Enhanced Solver for Geometry Problems" is available at Preprint.
[Dec 20, 2023] The project FormalGeo has been open-sourced.
[Nov 11, 2023] Paper "FormalGeo: An Extensible Formalized Framework for Olympiad Geometric Problem Solving" is available at Preprint.
[Nov 11, 2023] Welcome to FormalGeo homepage.
[Apr 18, 2023] We have been invited by Professor Hanchuan Peng to give an academic presentation at Southeast University.
[Apr 05, 2023] We have been invited by Professor Zhengfeng Yang to give an academic presentation at East China Normal University.

Publications

💥A Hybrid Framework for Automated Geometric Problem-Solving by Integrating Formal Symbolic Systems and Deep Learning
Zhengyu Hu, Xiaokai Zhang, Qin Cheng, Yang Li, Tuo Leng
To address the limitations of unidirectional approaches, we developed a neuro-symbolic system that integrates forward and backward reasoning.
Symmetry 2026 [Paper] [Project] [BibTex]
🔥FGeo-HyperGNet: Geometric Problem Solving Integrating FormalGeo Symbolic System and Hypergraph Neural Network
Xiaokai Zhang, Yang Li, Na Zhu, Cheng Qin, Zhenbing Zeng, Tuo Leng
We built a neural-symbolic system to automatically perform human-like geometric deductive reasoning. The symbolic part is a formal system built on FormalGeo and the neural part is a hypergraph neural network based on the attention mechanism.
IJCAI 2025 [Paper] [Project] [BibTex]
FGeo-Eval: Evaluation System for Plane Geometry Problem Solving
Qike Huang, Xiaokai Zhang, Na Zhu, Fangzhen Zhu, Tuo Leng
We propose FGeo-Eval, a comprehensive evaluation system for plane geometry problem solving. The evaluation system includes a problem completion rate (PCR) metric to assess partial progress, theorem weight computation to quantify knowledge importance, and a difficulty coefficient based on reasoning complexity.
Symmetry 2025 [Paper] [BibTex]
FGeo-Parser: Autoformalization and Solution of Plane Geometric Problems
Na Zhu, Xiaokai Zhang, Qike Huang, Fangzhen Zhu, Zhenbing Zeng, Tuo Leng
In this paper, we propose an enhanced geometric problem parsing method called FGeo-Parser, which converts problem diagrams and text into the formal language of the FormalGeo. Specifically, diagram parser leverages the BLIP to generate the construction CDL and image CDL, while text parser employs the T5 to produce the text CDL and goal CDL where these neural networks are both based on a symmetric encoder–decoder architecture.
Symmetry 2025 [Paper] [Project] [BibTex]
🔥Formal Representation and Solution of Plane Geometric Problems
Xiaokai Zhang, Na Zhu, Cheng Qin, Yang Li, Zhenbing Zeng, Tuo Leng
In this paper, we present formalgeo7k, a geometric problem dataset based on rigorous geometry formalization theory and consistent geometry formal system, serving as a benchmark for various tasks such as geometric diagram parsing and geometric problem solving.
NeurIPS 2024 Workshop on MATH-AI [Paper] [Project] [BibTex]
FGeo-DRL:Deductive Reasoning for Geometric Problems through Deep Reinforcement Learning
Jia Zou, Xiaokai Zhang, Yiming He, Na Zhu, and Tuo Leng
We built a neural-symbolic system, called FGeoDRL, to automatically perform human-like geometric deductive reasoning. The neural part is an AI agent based on reinforcement learning and the symbolic part is a reinforcement learning environment based on geometry formalization theory and FormalGeo.
Symmetry 2024 [Paper] [Project] [BibTex]
FGeo-TP: A Language Model-Enhanced Solver for Geometry Problems
Yiming He, Jia Zou, Xiaokai Zhang, Na Zhu, Tuo Leng
we introduced FGeo-TP (Theorem Predictor), which utilizes the language model to predict theorem sequences for solving geometry problems. Our results demonstrate a significant increase in the problem-solving success rate of the language model-enhanced FGeo-TP on the FormalGeo7k dataset, rising from 39.7% to 80.86%.
Symmetry 2024 [Paper] [Project] [BibTex]
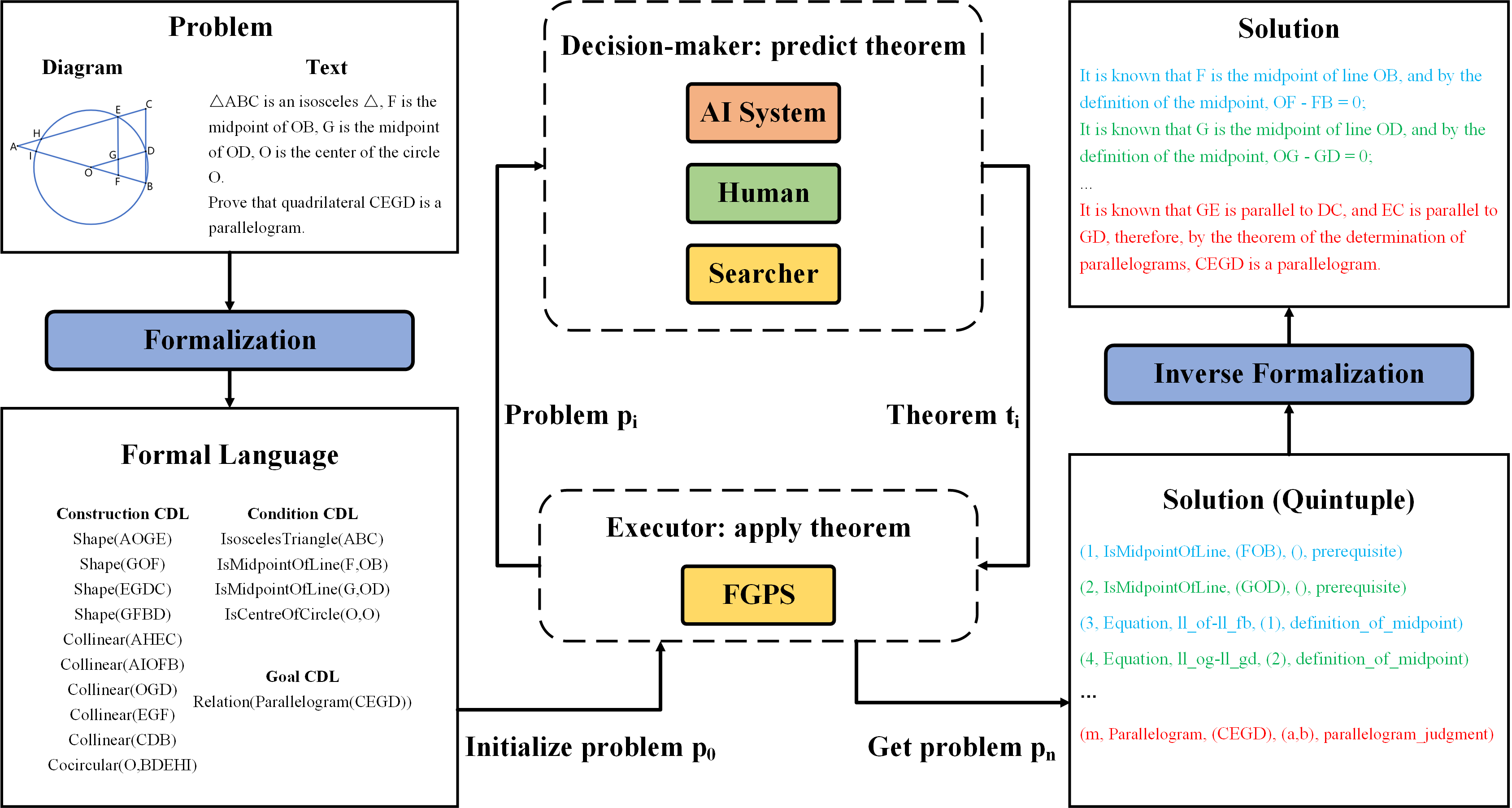
FGeo-SSS: A Search-Based Symbolic Solver for Human-Like Automated Geometric Reasoning
Xiaokai Zhang, Na Zhu, Yiming He, Jia Zou, Cheng Qin, Yang Li, Tuo Leng
Based on the geometry formalization theory and the FormalGeo geometric formal system, we have developed the Formal Geometric Problem Solver (FGPS) in Python, which can serve as an interactive assistant for verifying problem-solving processes and as an automated problem solver that utilizes a variable search-based method and strategy.
Symmetry 2024 [Paper] [Project] [BibTex]
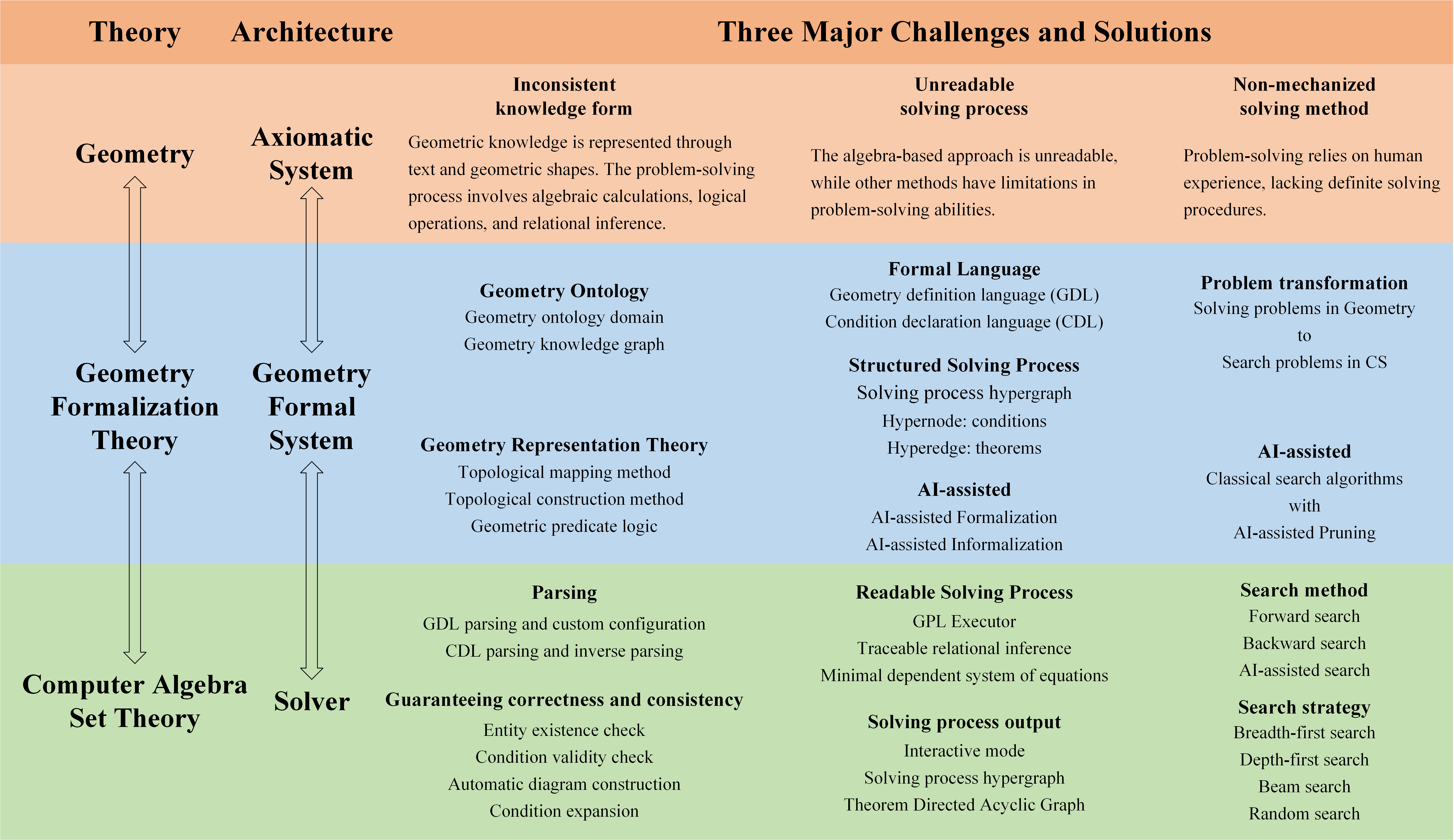
🔥FormalGeo: An Extensible Formalized Framework for Olympiad Geometric Problem Solving
Xiaokai Zhang, Na Zhu, Yiming He, Jia Zou, Qike Huang, Xiaoxiao Jin, Yanjun Guo, Chenyang Mao, Zhe Zhu, Dengfeng Yue, Fangzhen Zhu, Yang Li, Yifan Wang, Yiwen Huang, Runan Wang, Cheng Qin, Zhenbing Zeng, Shaorong Xie, Xiangfeng Luo, Tuo Leng
We have constructed a consistent formal plane geometry system. This will serve as a crucial bridge between IMO-level plane geometry challenges and readable AI automated reasoning. With this formal system in place, we have been able to seamlessly integrate modern AI models with our formal system.
arxiv:2310.18021 [Paper] [Project] [BibTex]

Extended Works

Hyuk Namgoong, Jeesu Jung, Yerim Han, Sangkeun Jung. When Does Auxiliary Modality Matter in Solving Geometric Problems? A Comprehensive Study of Textual, Formal, and Visual Modalities. In Proceedings of the 19th Conference of the European Chapter of the Association for Computational Linguistics (EACL 2026), Volume 2: Short Papers, 76–92. Rabat, Morocco, 2026.
Jo-Ku Cheng, Zeren Zhang, Ran Chen, Jingyang Deng, Ziran Qin, Jinwen Ma. GeoUni: A Unified Model for Generating Geometry Diagrams, Problems and Problem Solutions. In Proceedings of the 33rd ACM International Conference on Multimedia (MM '25), 3057–3066. Association for Computing Machinery, New York, NY, USA, 2025.
Yicheng Pan, Zhenrong Zhang, Pengfei Hu, Jiefeng Ma, Jun Du, Jianshu Zhang, Quan Liu, Jianqing Gao, Feng Ma. Enhancing the Geometric Problem-Solving Ability of Multimodal LLMs via Symbolic-Neural Integration. In Proceedings of the 33rd ACM International Conference on Multimedia (MM '25), 5394–5403. Association for Computing Machinery, New York, NY, USA, 2025.
Yurui Zhao, Xiang Wang, Jiahong Liu, Irwin King, Zhitao Huang. Towards Geometry Problem Solving in the Large Model Era: A Survey. In The 2nd AI for Math Workshop at the 42nd International Conference on Machine Learning (ICML 2025). Vancouver Convention Center, Canada, July 13-19, 2025.
Zeren Zhang, Jo-Ku Cheng, Jingyang Deng, Lu Tian, Jinwen Ma, Ziran Qin. Diagram Formalization Enhanced Multi-Modal Geometry Problem Solver. In 2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 1-5. Hyderabad, India, 2025.
Oren Sultan, Eitan Stern, Dafna Shahaf. A Neuro-Symbolic Approach for Reliable Proof Generation with LLMs: A Case Study in Euclidean Geometry arXiv preprint arXiv:2505.14479v7. Mar 2026.
Jiwan Chung, Neel Joshi, Pratyusha Sharma, Youngjae Yu, Vibhav Vineet. What MLLMs Learn about When they Learn about Multimodal Reasoning: Perception, Reasoning, or their Integration? arXiv preprint arXiv:2510.01719v3. February 2026.
Jingyun Wang, Dian Li, Xiaohan Wang, Gang Liu, Jiahong Yan, Guoliang Kang. Concise Geometric Description as a Bridge: Unleashing the Potential of LLM for Plane Geometry Problem Solving. arXiv preprint arXiv:2601.21164v2. February 2026.
Linger Deng, Yuliang Liu, Wenwen Yu, Zujia Zhang, Jianzhong Ju, Zhenbo Luo, Xiang Bai. GeoFocus: Blending Efficient Global-to-Local Perception for Multimodal Geometry Problem-Solving. arXiv preprint arXiv:2602.08524. February 2026.
Chengrui Zhang, Maizhen Ning, Tianyi Liu, Zihao Zhou, Jie Sun, Qiufeng Wang, Kaizhu Huang. GeoSDF: Plane Geometry Diagram Synthesis via Signed Distance Field. arXiv preprint arXiv:2506.13492v2. November 2025.
Yuhao Zhang, Dingxin Hu, Tinghao Yu, Hao Liu, Yiting Liu. GeoFM: Enhancing Geometric Reasoning of MLLMs via Synthetic Data Generation through Formal Language. arXiv preprint arXiv:2510.27448. October 2025.

Competitive Research

Chi Zhang, Jiajun Song, Siyu Li, Yitao Liang, Yuxi Ma, Wei Wang, Yixin Zhu, Song-Chun Zhu. Proposing and solving olympiad geometry with guided tree search. Nature Machine Intelligence 8, 84–95, 2026.
Trieu H. Trinh, Yuhuai Wu, Quoc V. Le, He He, Thang Luong. Solving olympiad geometry without human demonstrations. Nature 625, 476–482, 2024.
Google Deepmind. Advanced version of Gemini with Deep Think officially achieves gold-medal standard at the International Mathematical Olympiad. url: https://deepmind.google/blog/advanced-version-of-gemini-with-deep-think-officially-achieves-gold-medal-standard-at-the-international-mathematical-olympiad/

Members

Tuo Leng^1,2,3

Xiaokai Zhang^1,3

Yang Li^1,3

Cheng Qin^1,2,3

YuChang Yang^1,3

Zhenhai Sun^1,3

Zhengyu Hu^1,3

Ruiqing Xia^1,3

¹ School of Computer Engineering and Science, Shanghai University, Shanghai, China
² Institute of Artificial Intelligence, Shanghai University, Shanghai, China
³ Geometric Cognitive Reasoning Group, Shanghai University, Shanghai, China

Former Members

Na Zhu

Qike Huang

Jia Zou

Yiming He

Na Zhu, member, 2022.09 - 2025.06. She led the development of FGeo-Parser.
Qike Huang, member, 2022.09 - 2025.06. She led the development of FGeo-Eval.
Jia Zou, member, 2022.01 - 2024.06. He led the development of FGeo-DRL.
Yiming He, member, 2022.01 - 2024.06. He led the development of FGeo-TP.

Contact

Questions about FormalGeo, or want to get in touch? Email formalgeo@gmail.com, open up an issue on GitHub, or contact team leader Tuo Leng.